How is AI biased?

Many articles have been written about the increasing problem of ‘racist’ AI. But how come AI systems are biased in the first place? First, we must understand how these systems are trained.

Machine Learning

AI is basically a machine learning technique on stereoids: they take large amounts of data to create intelligent behaviour. Basic ML algorithms can do things like predicting housing prices, classifying data, and reducing the dimensionality of data (PCA, SVD, Fourier). [Explain dimensionality reduction] One problem we always face is how to set the parameters of our machine learning model.

During training of a model, such as a deep neural network, we need to optimize the weights. We do this by feeding the model with information in form of input data. This could be images, text, or even speech. At the beginning of training the input data gets passed through the network. We call this the feedforward pass. The input is transformed into numbers (e.g. a numerical representation of images would be a list of numbers - the pixel values) and undergoes various processing steps before the network returns an output. We then compare this predicted output to the actual input. We typically denote the output as y and the input as x_i.

When we compare the prediction to the actual input we compute the error the network made - the bigger the error, the more it must be punished (or trained). We do this via the backward pass which is known as backpropagation. To keep it simple: backpropagation simply adjusts the weights in each layer by multiplying a weight w_n by some amount. The larger the error, the larger this update to the weight. Repeating this procedure of feedforward and backward passes enough times, results in a network whose weights are tuned towards the data we’ve used as input. The idea is that the model is now able to approximate this data.

When we feed it new data which it hasn’t seen before, we expect it to classify it correctly based on its trained weights. However, the training procedure poses a big problem: how do we fit the model to the data just the right amount as to not limit ourselves to only just data?

This is where bias comes into play: the more biased a network is, the more it fits the data it was trained on. For example, if the majority of input data used for training involves criminal cases which consist largely of african-american repeat offenders [CITE], it will tune it’s weights to fit that distribution; the result is a model which will predict, based on its training, that an african-american will be more likely to engage in criminal acitvities again.

In machine learning we make a trade-off between bias and variance. The variance describes how large the error is between our prediction and the actual values; low variance means that the network or model is overfit. This bares the risk of performing well on training data, but not being able to generalize to new input data. High variance is the opposite. Bias on the other hand controls how much error the network causes by missing important connections in the data. Both control how well the network will generalize to new input.

The dilemma is that ‘racist’ AI is in reality a biased AI: it was incorrectly & insufficiently trained on the data.

Future research should explore the bias/variance trade-off and find ways to optimize training data for representability & lack of underlying assumptions. However, it should also explore the benefits that may arise from ‘stereotyping’: it is possible that despite the negative implications for socioeconomic based issues, such as income, gender or race, stereotyping offers a valuable way for quickly categorizing novel instances by making use of heuristic assumptions. In this respect, deep meta-Reinforcement Learning offers a promising avenue, due to it’s approach of creating cognitively nimble AI with deep sophisticated knowledge.

1. Cortical neurons do not communicate real-valued activities
   1. What are real-values?
      1. Numbers such 3.14 or 2/5 or -6.9.
      2. In neural networks we use vectors of these numbers to represent the weights of the different layers.
         1. For example, the first layer is a vector w₁ n real values. The first value might be 0.92, the second value 0.2 and so on until the n-th value. These are the weights of w₁.
      3. Neural networks use these weights to communicate information
         1. The weights are essentially the input to a function. Each weight is passed to a function as an x value (e.g. $f(x)$).
         2. The function $f(x)$ can be for example a sigmoid or a Rectified Linear Unit (ReLU).
         3. A neural network uses hundreds of these functions in each layer. This allows it to learn from input - by passing in different values for x we get different positions on the function.
            1. We hope that by using the right activation function we will be able to abstract the information in the input. For this we need to translate it into real-values.
   2. How do neurons communicate
      1. Neurons communicate via spikes i.e. electrical activity
      2. What are action potentials?
2. Neurons need to two send two types of signals
   1. forward
   2. backward
      1. backpropagation only passes backwards
   3. neurons in ANNs do not send activity forward AND backward
      1. Recurrent Neural Networks
3. Neurons do not have point-wise reciprocal connections with the same weight in both directions
   1. Nodes in ANNs have connections to multiple neurons with different weights
      1. however the weight from a single node_A to a node_B is the same both ways (i.e. from A to B and from B to A)
   2. Neurons have connections to various different neurons - the reciprocal connections have different weights as well
      1. e.g. a sending neuron might have a larger weighting than a backpropagating neuron –> backpropagation does exist - just not in a purely mathematical form, nor as a unique mechanism
      2. parallel weight assignments - neurons can have reciprocal connections with different weights, allowing for parallel forward passing as well as backpropagation

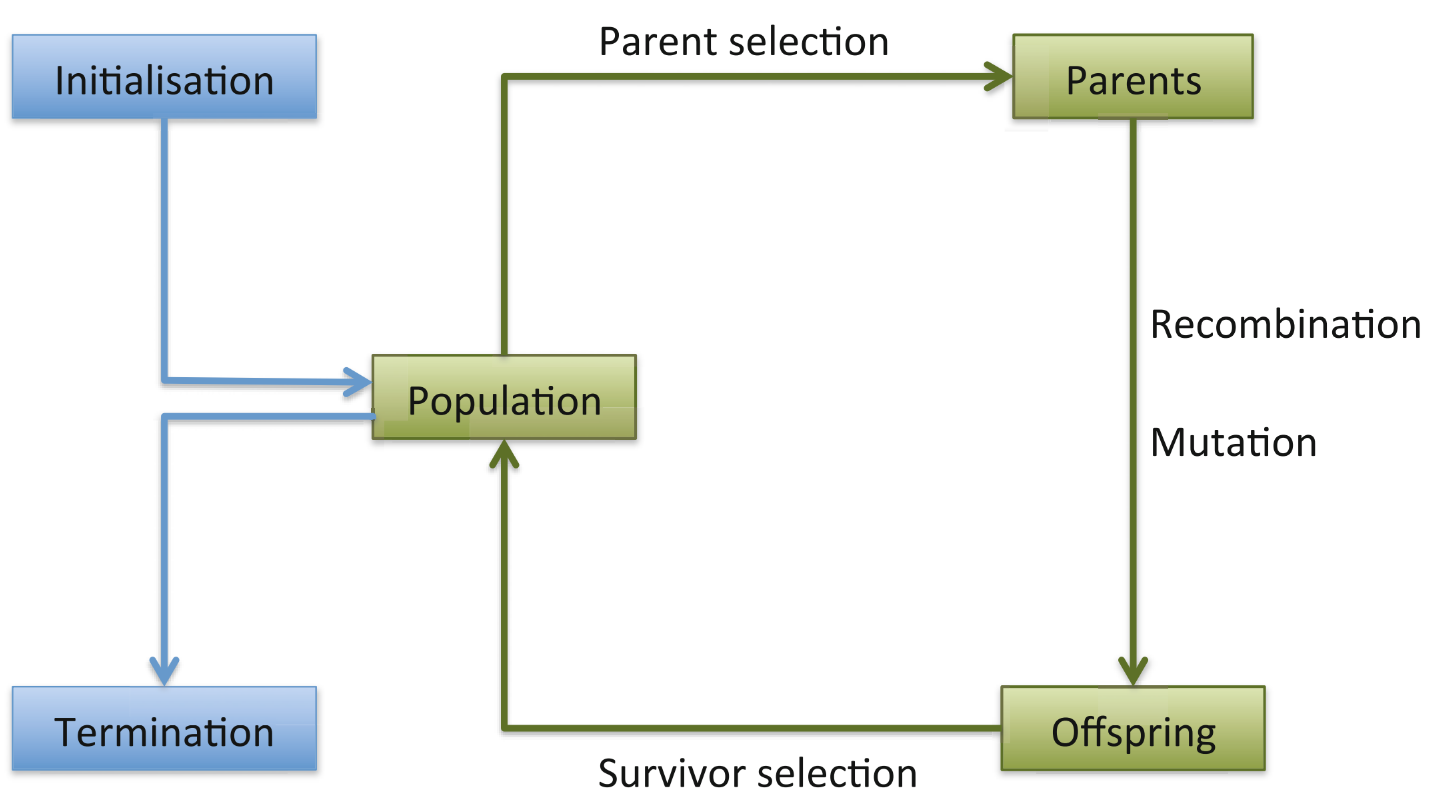
What is Evolutionary Computing

Evolutionary Computing is a fascinating method for solving problems. It is inspired by biological evolution, which operates under the principle of ‘survival-of-the-fittest’: in an environment with limited resources, populations of individuals compete and mate to produce the fittest offspring. This process repeats over multiple generations.

While biological evolution is complicated through bio-chemical processes, EC can be broken down into several, simple steps.

What is finance and why do we need it?

Finance is, in its essence, a technology. It is the driving force behind getting people to do things.

Organizations

In the world of finance - that is: in our world - we can not achieve much as individuals. This is a fundamental principle of life. To make a change in this world, we need to build connections and become part of a collective. We call these collectives of people organizations. They will help us accomplish much greater things than we could by doing everything by ourselves.

Topics in Finance

Finance covers a broad range of topics. When people hear the word “finance” they typically think about the stockmarket, real estate, or banking. It actually composes far more than that. In finance we deal with risk assessment, debt management, insurance, diversification of assets, regulation of markets, trading futures, public finance, and behavioural finance. The latter is related to studying the psychology of how people make financial decisions. There are many more topics not covered, but these represent a broad overview of what finance really deals with.

Finance as a technology

It is important to understand that finance is not just a theory or a field of study. It is a technology, like a computer. We can use a computer to perform certain tasks; similarly with finance. Like any technology, finance can be used for good or for evil. Philantropism is an example of good finance - it involves people who have accumulated a lot of wealth, spending their hard-earned money for the benefit of society. Greedily hoarding money and passing it down one’s own lineage is the opposite of philanthropism and represents the evil side of finance.

However, there are some types of finance that have good intentions but unintended outcomes. Foreign aid, for example, is the support of developing nations by providing them with money. Yet, obtaining money is not the main interest of developing nations. Primarily, they are interested in our financial technologies, that is, they want to understand what principles they need to establish, to model the financial success of Russia, China, Germany, or the USA.

Ethics of Finance

Finally, there are the morals of finance. People who will become wealthy, are people who have a “natural, practical talent”. The business world essentially selects people based on their skills - this happens naturally. People who want to do good things for the world have a mindset which will lead them to success. They will find ways to obtain & amass wealth as to obtain their goals. However, they will be obligated to spend their wealth for the benefit of society - not on their (spoiled) children!

Money without purpose is evil money. According to Andrew Carnegie, the second stage of life of an wealth person is to retire early and become a philanthropist. By mastering the principles underlying finance, anyone can become wealthy and help society succeed in its pursuit for knowledge, power, and technology.

Black Box

A black box is a box where you put something and get something out. You do not know what happens inside the box, only what you put in - the input - and what comes out: the output. We use this view to describe computer systems where we are not quite sure what is going on inside. This is a common problem in neural networks, and especially deep neural networks. DNNs consist of many layers of computation and we often do not know what happens inside them. For example, how can a network say that our cat picture has a cat in it and our dog picture a dog?

When we develop a neural network or some other type of problem-solving algorithm, it is good to know what kind of problem we are dealing with exactly. Are we trying to find an input which fulfills some sort of requirement? Or are we looking for a model which is great at predicting stockprices? The black box view of computational models helps us identify these problem types, by distinguishing between 3 components: the input, the model, and the output.

Optimization

If the input is not known, then we are dealing with an optimization problem: we only have the model and the output to our disposal. A typical problem is the travelling salesman problem: how can we visit all the cities in a region with a limited amount of moves? The goal is to find the input which optimizes this requirement; i.e. it finds the shortest sequence to visit all the cities. You may realize how finding the shortest sequence of any input can be quite useful across a wide range of problems: finding the shortest route on Google Maps, creating layouts for buildings, or creating schedules. What happens, however, when we have no idea what the model should look like in the first place?

Modelling

Modelling problems require us to estimate the unknown model by using inputs & outputs. After providing enough inputs we hope that the model learns some pattern so that it can predict future inputs’ values. This type of problem is useful for building a stocktrading bot; here, we need to find a model which can predict stock prices (output) based on historical stock data (input). Another example would be image recognition, where we label images, feed them to our model, and hope to find a model which can correctly label new, unlabelled images. Interestingly, we can transform modelling problems into optimization problems: instead of asking for a model m which accurately maps an input x to its label y, we can attempt to find a model m which makes the least amount of mistakes. You may have noticed that this implies that if we find a solution to a optimization problem, we have also found a solution to our modelling problem, because we have found a model (modelling) with optimal performance (optimization).

Simulation

Lastly, if we do not know what the output of our model is supposed to be, we can phrase it as a simulation problem. This is quite useful for studying the effects of self-driving cars, for example. Instead of unleashing untested algorithms out on the street, we can have them spend millions of virtual miles behind a driving simulator to assess their performance. Because we are using a simulation, we have much more control over the different variables, the amount of experiments we can do, and the amount of testing data we can generate. This makes simulations much less expensive than conducting research in real world environment, which is also associated with great risks. However: no simulation is perfect, and the results should never be considered to be realistic. At best they are a proof-of-concept.

By using the black box view to classify a problem-at-hand as either a optimization, modelling, or simulation problem, we can take some of the guesswork out of our research. Understanding this view can help immensely in starting to think more pro-actively about what the goal of our model or system is supposed to be.

This is a hello world post.